Card image Card image

Accelerating industrial legacy robot manipulation

TEKNIA, an auto parts manufacturer, wanted to speed up their existing robots for faster production cycles. We collaborated to achieve first a 16.21% increase in robot movement speed by introducing variations of the robot trajectories, velocities and accelerations, and later, on a second stage a 10.78% decrease in cycle time via double-manipulation. Leveraging modern techniques, we pushed the boundaries of the robot's velocity and acceleration with optimized machine-robot interactions and movements (paths and speed), ensuring efficient movement paths with minimal wasted motions. These improvements empowered TEKNIA to produce an additional 800 units per day and over 20,000 units per month.

The challenge

Metallic tubes are manufactured in a continuous process, while going through various stages of production. A robot is used to manipulate the tubes and move them from one stage to another. The robot's speed and acceleration are limiting factors in the production cycle.

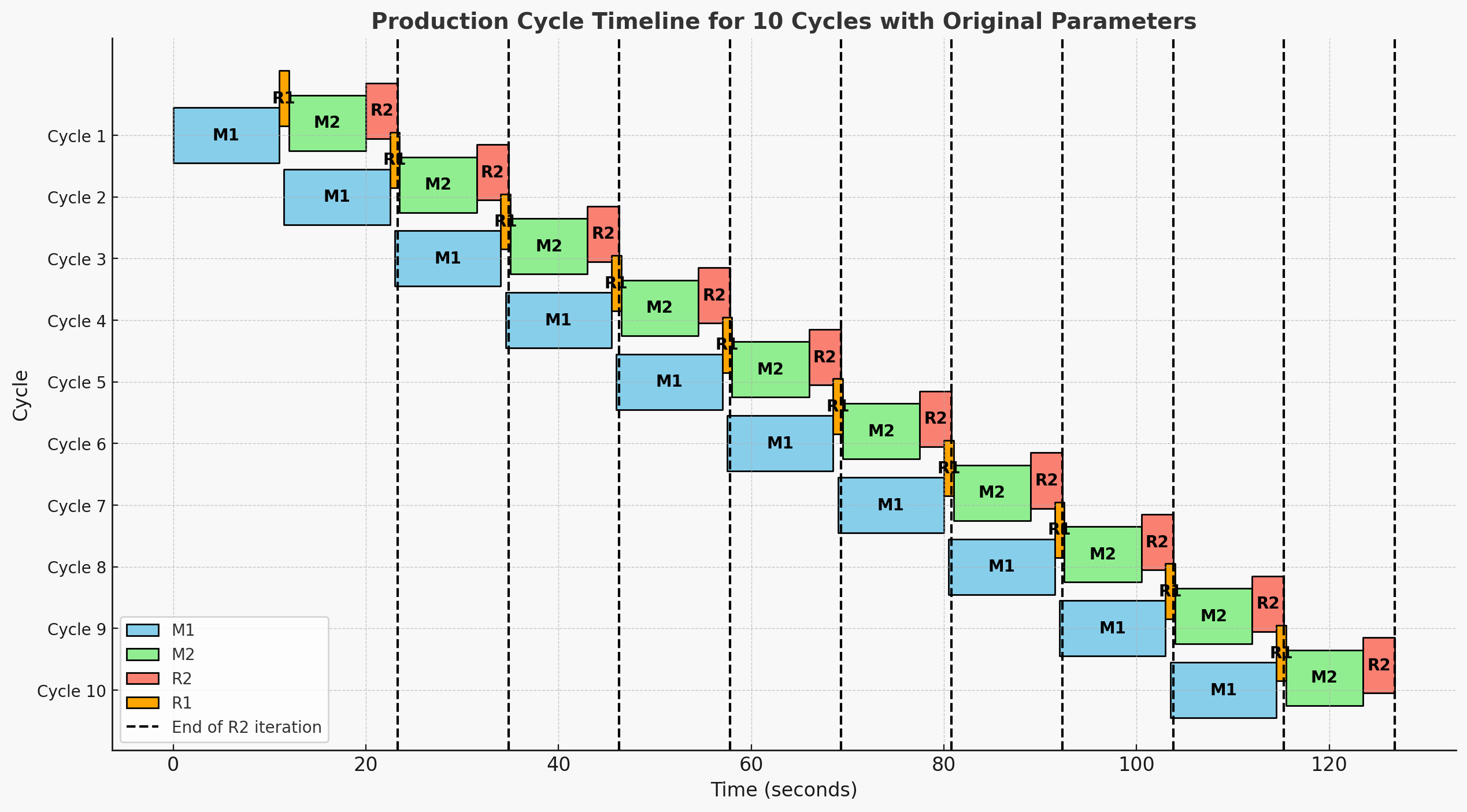
\[ \text{First (n=1):} \begin{cases} T_{\text{start}}^1(M_1) = 0 \\ T_{\text{end}}^1(M_1) = T_{\text{start}}^1(M_1) + T_{M1}\\ T_{\text{start}}^1(R_1) = T_{\text{end}}^1(M_1) \\ T_{\text{end}}^1(R_1) = T_{\text{start}}^1(R_1) + T_{R1} \\ T_{\text{start}}^1(M_2) = T_{\text{end}}^1(R_1)\\ T_{\text{end}}^1(M_2) = T_{\text{start}}^1(M_2) + T_{M2} \\ T_{\text{start}}^1(R_2) = T_{\text{end}}^1(M_2) \\ T_{\text{end}}^1(R_2) = T_{\text{start}}^1(R_2) + T_{R2} \\ \end{cases} \]

\[ \text{Subsequent (n} \geq \text{2):} \begin{cases} T_{\text{start}}^n(M_1) = T_{\text{end}}^{n-1}(R_1) - T_{M1\_overlap} \\ T_{\text{end}}^n(M_1) = T_{\text{start}}^n(M_1) + T_{M1} \\ T_{\text{start}}^n(R_1) = T_{\text{end}}^n(M_1) \\ T_{\text{end}}^n(R_1) = T_{\text{start}}^n(R_1) + T_{R1} \\ T_{\text{start}}^n(M_2) = T_{\text{end}}^n(R_1) \\ T_{\text{end}}^n(M_2) = T_{\text{start}}^n(M_2) + T_{M2} \\ T_{\text{start}}^n(R_2) = T_{\text{end}}^n(M_2) \\ T_{\text{end}}^n(R_2) = T_{\text{start}}^n(R_2) + T_{R2} \end{cases} \]

Mathematical
formulation

Given the constraints of the robot, we formulated a mathematical model to optimize the cycle time. We considered the various possibilities, involving the various involved machines, a faster-moving robot, and also multiple robots. We then used this model to determine the optimal combination of the interactions between the robots and the connected machines in the automation line.

Modeling the
time-series

We modeled the time-series of the robot movements and the machine interactions to optimize the cycle time of the automation line. This allowed us to determine the optimal combination of the interactions between the robots and the connected machines in the automation line.

Before
Before After

Digital twin-driven
validation

We used digital twins to co-develop and validate the optimal time-series model. This allowed us to simulate the robot movements and the machine interactions in a virtual environment, ensuring the optimal cycle time of the automation line.

Reducing the reality gap in digital twins

We reduced the reality gap in the digital twin which allowed us for faster iterations between the real world and the digital twin. This enabled us to optimize the robot movement speed for real-world performance.

Result 1:
16.21% faster
robot movement

On a first iteration, we achieved a 16.21% increase in robot movement speed by means of modifying trajectories and movements (velocities and accelerations), enabling TEKNIA to speed up their production cycles and increase their manufacturing capacity.

Result 2:
10.78% faster with
dual manipulation

We were further challenged to increase the productivity, so we proposed a dual manipulation system. This system allowed for synchronous multi-robot trajectory coordination leading to a 10.78% increase in the manufacturing cycle time.

+800
units/day

+20K
units/month

We're here to help

Let us help accelerate your robots.

Let's talk Case studies